Specific Research Projects
Physical, geophysical, chemical, living and human-made systems often show behaviors that cannot be understood by studying their building blocks or constituents to ever finer detail but that are emergent. The concept of emergence can be summarized by the statement that there exists an entity (e.g. an organism) which is more than the sum of its parts. This is often used as the defining property of a complex system. Many of these complex systems can be represented as a collection of dynamical units coupled via complex architectures. Complex network theory offers a unified description of these complex systems and has been invaluable in discovering unifying characteristics and principles despite the intrinsic differences between systems. Understanding these emergent characteristics and principles, their stability and the selforganization processes leading to them is one of the central quests of modern physics. Prominent examples include seismicity and neural signaling or biological signaling processes in general, with immense importance for society. A detailed understanding of seismicity is required to ensure successful seismic hazard assessment and to explore the possibility of successful earthquake prediction. A detailed understanding of the brain is essential to tackle brain related diseases such as Alzheimer's and epilepsy.

Spreading & triggering processes
Spreading processes, triggering cascades or information cascades play an important role in many complex systems as observed, e.g., in rock fracture, seismicity and neurodynamics. In the case of earthquakes, these cascades can be considered synonymous with the classical main shock-aftershock paradigm — one event triggers other events, which in turn trigger secondary events etc. as in a mathematical branching process. In the case of neuronal systems, triggering is the process by which information spreads as individual nerve cells activate others. Often the properties of triggering cascades resemble those encountered in phase transitions in equilibrium systems characterized by self-similarity, critical exponents, scaling functions etc. In non-equilibrium settings, a similar general framework of criticality is still missing. Moreover, understanding the underlying principles behind the emergent properties of triggering cascades are also important for seismic hazard assessment as well as for a better understanding of brain-related diseases such as epilepsy and Alzheimer’s.
Fluid-induced seismicity
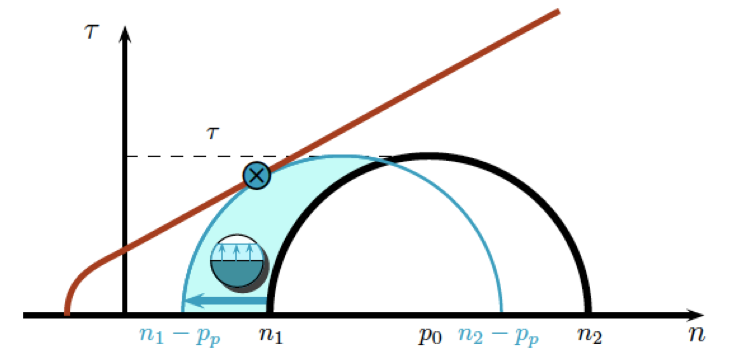
Variations in pore pressure due to fluid invasion in stressed materials can activate processes of mechanical failure, such as the initiation, propagation and coalescence of fractures, or the slip of frictional surfaces in pre-fractured faults. This phenomenon accounts for (micro-)seismic activity recorded in natural settings, stimulated geothermal systems, during hydraulic fracturing operations, and following the underground disposal of wastewater. Conceptual models explain how failure can be induced by variations in the applied stress tensor and pore pressure stimulated by highly pressurized fluid injection. The magnitudes of fluid-induced seismicity are typically low, which is often challenging to detect on the surface and well below the threshold for being felt. However, in some rare cases these processes can activate nearby faults and trigger stronger events.

Computational neuroscience & the critical brain
The brain is a prime example of a complex system: It is composed of interconnected parts — neurons — that as a whole exhibit properties (behavior among them) not obvious from the properties of the individual parts. From a philosophical point of view, this is related to fundamental questions of free will and consciousness, for example.
Much like a computer, the brain receives, processes and outputs information. The brain's tremendous complexity makes an immediate understanding of its dynamics an overwhelming task. However, studying the dynamics of much smaller groups of neurons appears to be a promising first step. Currently, researchers are able not only to culture neuronal networks on silicon wafers, but also to send information to specific neurons in these circuits and to read out information – by optically recording the resulting cascade of activity. It is well known that the neurons' activity can influence their connectivity by rewiring the synaptic connections between them. By learning how this neuronal plasticity is used to achieve cognitive function we may also learn how to "program" these neuronal cultures into massively parallel bio-computing devices. These neuronal networks have the potential to excel in areas where conventional computers have struggled, such as pattern recognition and complex decision making.
Progress in understanding the basic principles of neuronal dynamics is needed to make these breakthroughs a reality. The apparent homogeneity and dense interconnectivity of the vast number of neurons in neuronal tissue make it well suited to analysis using techniques from statistical physics and complex network theory. Applying these tools to neuroscience is certainly not a new idea; however, with the advent of new high quality data sets warrants a reinvestigation of some existing ideas and opens up room for new ones.
Specifically, hallmarks of criticality, such as power-laws and self-similarity typical for order-disorder phase transitions, have been found in many neuronal systems. Synchronization patterns have been shown to exhibit broadband criticality; critical avalanches of spontaneous neural activity have been found both in vitro and in vivo, and results from large-scale brain models based on the human connectome show that only at criticality the brain structure is able to support the dynamics observed in functional magnetic resonance imaging. All this evidence suggests that criticality — potentially emerging not in the form of a critical point but rather as an extended critical region — might have a relevant role in brain dynamics. This is supported by the conceptual picture that the brain cannot be in a noise-dominated disordered state or in a almost static ordered state but must operate somewhere between these two extremes to ensure coherent functioning while allowing flexibility to adapt to varying conditions. In particular, it has often been argued that criticality in the brain implies optimal transmission and storage of information, optimal computational capabilities and maximal sensitivity to stimuli.

Rock fracture & frictional sliding
The mechanical failure of natural or man-made structures due to the variations of the external loads or long exposure to extreme external conditions constitutes a common hazard of major concern in seismology and civil engineering. Experimental studies reveal that the mechanical deformation of crystalline structures, amorphous materials, and jammed granular (or fragile) matter is highly affected by the inherent heterogeneity in the system or some degree of disorder such as defects, dislocations, or inclusions. Hence, failure is difficult to forecast because of the sensitivity to the unknown internal details of the system. In micromechanical models of failure, the addition of disorder is able to arrest the internal micromechanical processes responsible for deformation in multiple metastable states, leading to stochastic avalanche dynamics. The arrested energy is partially released during the mechanical avalanche as elastic waves that can be detected by means of seismographs and geophones at the geological scale, or by ultrasonic acoustic emission (AE) equipment in laboratory controlled experiments. Such elastic waves can be used as probes to assess the state of the system and develop reliable forecasting tools for structural health monitoring.

Statistical seismology
One of the major hurdles in studying earthquake interactions is the fact that the physical processes corresponding to an earthquake can not be viewed directly due to the opaque interior of the earth. This necessitates inferring relevant information on the underlying earthquake dynamics from the ongoing evolving patterns of seismicity and structures of fault networks. Specifically, clustering is a prominent hallmark of seismicity and fault patterns. Clustering in space is exemplified by the concentration of earthquakes along the boundaries of tectonic plates. Spatiotemporal clustering is best seen as a significant increase of local seismic activity immediately after large earthquakes, within so-called aftershock sequences. The clustering of activity remains one of the primary sources of information for constraining physical models of earthquake dynamics, highlighting the important connection between statistical features and the underlying physics.
What is the dominant physical mechanism for earthquake-earthquake triggering in the near-field? Our work solved a long-standing controversy showing that field observations from Southern California are consistent with models relying exclusively on static stress triggering.

Network neuroscience
Understanding the principles and mechanisms underlying complex brain function and cognition is one of the major challenges of our time. The field of network neuroscience aims to tackle this challenge by an intuitively appealing framework that allows one to map observations to a mathematical description rooted in graph theory. On the level of the whole brain, functional Magnetic Resonance Imaging (fMRI) is often used as a specific way to measure the neural activity through changes in the Blood Oxygen Level Dependent signal. Specifically, a Resting-state functional Magnetic Resonance Imaging (Rs-fMRI) is obtained when the subject is in an awake state but not doing any task. The data obtained through Rs-fMRI are then typically used to estimate the interactions between different brain regions and a network representation is derived—different brain regions correspond to nodes in a graph and links between them represent interactions.

Synchronization & chimera states
One of the pillars of modern physics is the concept of symmetries. Spontaneously breaking such symmetries typically gives rise to non-trivial phenomena and can explain, e.g., why particles have mass. The occurrence of such symmetry-breaking phenomena is not limited to particle physics but occurs across a wide range of physical, chemical and biological systems. Recently discovered examples include chimera states. Chimera states are hybrid states characterized by the coexistence of localized synchronized and unsynchronized dynamics in a given system. Indeed, the name chimera is used here in analogy to the hybrid creature in Greek mythology. Such coexisting behavior can even occur in a homogeneous system, thus breaking the underlying symmetry - something that was long thought to be impossible. While over the last 10+ years a significant understanding of this phenomenon has started to emerge, many challenges are left to be addressed. E.g., since synchronization of oscillations, including nonlinear waves, is often a crucial part of the biochemical mechanisms responsible for biological function, chimera states have been proposed as a candidate to control certain biological functions. As a first step in this direction, we have shown that spiral wave chimeras - spiral waves with spatially extended unsynchronzied cores - can exist in biochemically relevant systems, that cannot be reduced to simple phase oscillators. Moreover, we have also shown for the first time that if the system is three dimensional - which is the relevant situation for many natural biochemical processes - novel chimera states can arise in the form of knotted and linked filaments.

Sociophysics
Animals, including humans, form social hierarchies or networks. How these hierarchies form and what makes them remain stable over time is a central question across many different fields. Specifically, the emergence of complex network structures and non-trivial global phenomena from local interactions is one of the main challenges in the field of complex network theory. For acquaintance networks, we have identified the essential dynamical ingredients necessary to obtain major non-trivial topological features like short path length, high clustering, and scale-free or exponential link distributions. Our model based on these ingredients compares well with observational data of social networks and has stimulated over 400 related studies on the evolution of networks. In particular, it has been shown by others [see P. Klimek and S. Thurner, Triadic closure dynamics drives scaling laws in social multiplex networks, New Journal of Physics 15 (2013) 063008] that our model and the dynamic process of triadic closure it is based on provides a natural explanation for several scaling laws related to structural characteristics of social networks. This indicates for the first time that these scaling laws are inter-related and a consequence of a common fundamental dynamical principle: triadic closure.
Climate dynamics & climate networks
There has recently been a large push to use complex networks to help understand climate dynamics. Complex networks have been used to analyze long-range correlations (teleconnections), climate models, phenomena such as El Nino, and continue to be of active interest. Typically, climate dynamics are mapped to networks by taking a set of global positions as nodes, and adding a link between any two that satisfy a specified criteria. The resulting networks, and their changes in topology over time, can then be analyzed to make inferences about the dynamics.

Extreme events and records
History often turns on extreme events, be they man-made or natural. Examples are global financial crises, military strikes or radical political events, or natural disasters such as floods and earthquakes, in the latter. Extreme events are often associated with catastrophes, and the word ’extreme’ is sometimes substituted by ’freak’ to suggest something unnatural and undesirable, or ’rogue’ in the case of ocean waves. Generally, the economic and social consequences of extreme events are a matter of enormous concern.
When such catastrophes strike, it is easy to look back and analyze mistakes. But how do we gain a better understanding that can be applied towards the next event? It is often argued that extreme events are so implausible as to be negligible for planning purposes. Of course, extreme events are, by their definition, rare. However, what is rarer still is that a rare event never occurs at all. In particular, extreme events have a number of key characteristics that are found over and over again. We know that records must be broken in the future, so if a flood design is based on the worst case of the past, then we are still not prepared for possible floods in the future. Materials will fail due to fatigue, so if the body of an aircraft looks fine to the naked eye, it must still fail seemingly out of the blue if the aircraft has been in operation over an extended period of time.
Much of science has concentrated, until recently, on understanding the mean behaviour of physical, biological or social systems and their “normal” variability. Extreme events, due to their rarity, have been hard to study and even harder to predict. The science of extreme value statistics aims to describe the occurrence of extreme events in a general and unified way. We focus on extreme value statistics suitable for cases where individual events are correlated with each other over a wide range of spatial and/or temporal scales. Such complex behavior arises due to nonlinear interactions between the components of the system and has recently been established as a general and significant phenomenon, space weather being one particular example.
Space weather arises from the interactions of solar activity, solar wind and Earth’s magnetosphere, with phenomena ranging from magnetic storm activity on short time scales to possible relationships with global warming on long time scales. Magnetic storm intensities and other space weather-related phenomena must be considered when designing ground-based electric power systems. The severe geomagnetic storm and associated province-wide power blackout in Quebec on 13 and 14 March 1989 illustrates the deleterious effects of extreme space weather activity on critical infrastructure systems.
We showed for the first time that well-defined extreme bursts exist in the solar wind that share many scale-free properties with their counterparts in solar activity. In addition to providing evidence for the direct influence of solar activity on the solar wind, our analysis also raised important questions in the context of the solar wind-magnetosphere interaction. For example, do such scale-free extreme bursts play a role for this interaction?

Pattern formation & cardiac arrhythmia
Many of the properties of macroscopic systems driven out of equilibrium by flows of matter and/or energy are not merely an additive effect. Instead, these properties emerge from cooperative interactions of their constituents, having no direct counterpart in the properties or dynamics of the microscopic constituents considered in isolation. While there is a general understanding of how such emergent properties arise in equilibrium — phase transitions, such as occur in the boiling or freezing of a liquid, and their description by renormalization group theory are one of the prime examples — this is not the case for systems far away from equilibrium.
A particularly interesting class of such self-organized structures are nonlinear waves. They occur in a multitude of systems including chemical and biological systems. For example, if chemical reagents are continuously supplied to and removed from a container where an oxidation reaction takes place on a catalytic surface, in many circumstances the chemical reaction does not occur homogeneously over the entire surface but instead proceeds by the propagation of chemical waves of oxidation that travel across the catalytic surface. The combination of nonlinear chemical kinetics and conditions that force the reaction to occur in far-from-equilibrium conditions is responsible for the existence of the evolving patterns of chemical waves seen on the surface of the catalyst. Similarly, in biological systems the nonlinear chemistry associated with biochemical networks, in combination with diffusion of chemical species, can lead to the formation of chemical waves which are often implicated in the mechanisms responsible for biological function as well as cardiac arrhythmia.
Nonlinear waves can also undergo instabilities leading to complex spatiotemporal chaotic states — states where a high-dimensional dynamical system is temporally chaotic and spatially irregular. Substantial efforts have been made to characterize these states but a complete and unified theory of such states still eludes us. In many of these cases, spatiotemporal chaos can be dominated by regions of local order centered around topological defects or phase singularities. In this case, it is typically called defect-mediated turbulence and the dynamics of the pattern is characterized by the rapid motion, nucleation, and annihilation of these defects. Defect-mediated turbulence appears in a wide range of processes including cardiac fibrillation — a disorganized electrical wave activity that destroys the coherent contraction of the ventricular muscle and its main pumping function leading to sudden cardiac death.
Boolean networks
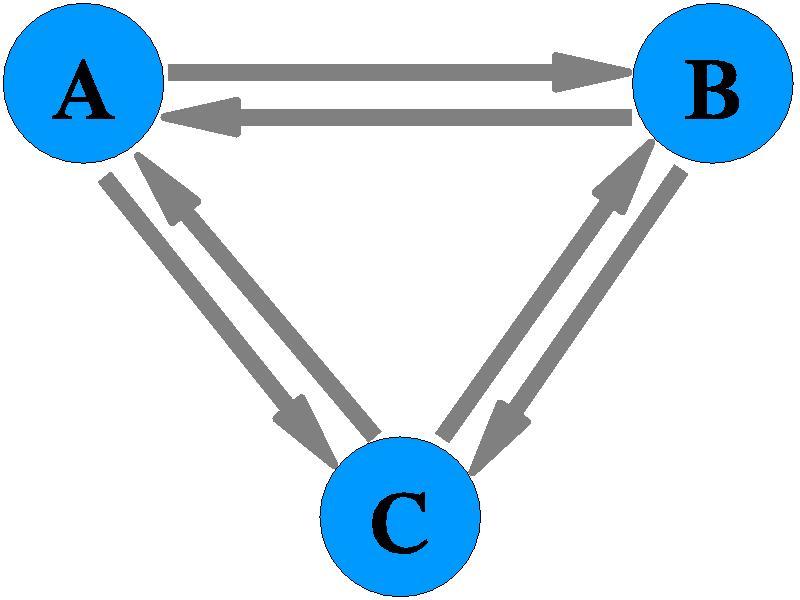
Random Boolean networks were originally introduced as simple conceptual models for genetic regulatory systems. The contrast between their simple design and their complex emergent behaviour has motivated researchers in diverse fields including the biological, neurological, computational and evolutionary sciences to use these or related models as test beds for ideas about self-organization. Complimentary to their application as models, this dichotomy between their straightforward formulation and their complex dynamics make them worthy of study in their own right.
The dynamics of Boolean networks can be represented by a directed state space network by linking each dynamical state, represented as a node, to its temporal successor. Like all finite discrete deterministic systems the dynamics must eventually settle into a periodic attractor cycle. We clarified how different weighting schemes, sampling methods and updating schemes (synchronous vs. asynchronous) affect the estimates for attractor length distributions, basin entropy and other observables in random and biological Boolean networks, . We showed that a number of measures commonly used to indicate criticality fail, while we also proposed and established the validity of other measures.
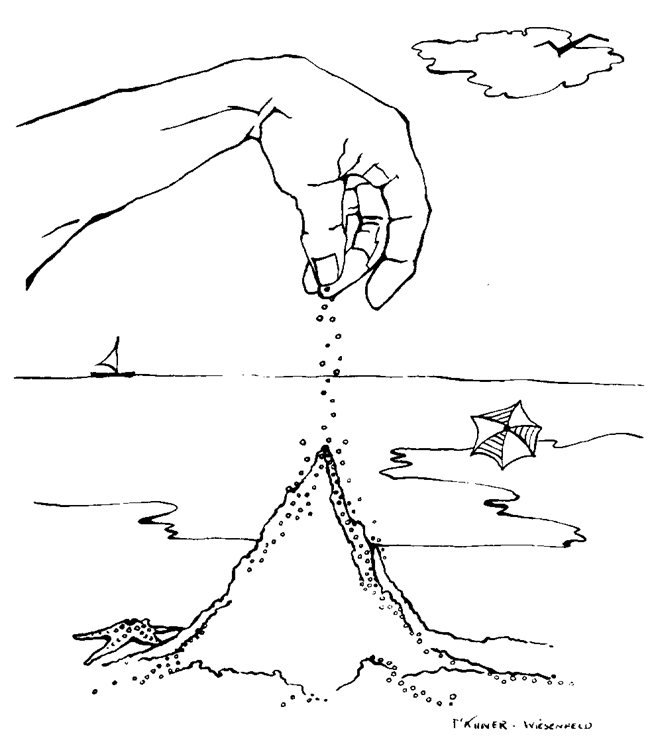
1/f noise and self-organized criticality
The ubiquity of 1/f noise or 1/falpha noise in nature is one of the oldest problems in contemporary physics still lacking a generally accepted explanation, despite much effort. The phenomenon is characterized by a 1/falpha decay with a nontrivial a found in the power spectrum of a given time signal at low frequencies. In many cases, the time signal describes a transport process. Then 1/falpha noise is an indication of anomalous behavior compared to conventional transport, as for instance, equilibrium diffusion. Flicker noise has been observed in a huge number of diverse systems, many of which are far from equilibrium and show a bursty, avalanche dynamics. Examples include earthquakes, combustion fronts, chemical reactions, flux motion in superconductors, and Barkhausen noise, to name only a few.
We demonstrated explicitly that the concept of self-organized criticality can provide a dynamical mechanism which gives correlations between bursts leading to 1/falpha noise. Our observations constituted the first proof of principle that a self-organized criticality mechanism can give low-frequency 1/falpha noise without imposing temporal correlations in the external drive.
In the context of neuroscience, we also presented a simple stochastic mechanism which can generate pulse trains exhibiting a power-law distribution of the pulse intervals and a 1/falpha power spectrum over several decades at low frequencies. Our proposed mechanism agrees with recent experiments in neurobiology and can explain the high interpulse interval variability and the occurrence of 1/falpha noise observed in cortical neurons.
