Aug. 20, 2014
Vaniers: Muhammad Ali Khan leverages power of mathematics

Ali Khan is the Department of Mathematics and Statistics’ first-ever Vanier Scholarship recipient.
Muhammad Ali Khan
Want to increase the profits of your investment portfolio? Need to efficiently assign staffing resources to limit emergency room wait time? Wondering how to optimize the potato production on your farm? These are the types of problems Muhammad Ali Khan, a PhD student in mathematics and recent Vanier award recipient, loves to dwell on and solve.
Born in Lahore, Pakistan, Khan moved to Calgary in September 2013 and is the first-ever Vanier Scholarship recipient from the Department of Mathematics and Statistics. “I love tackling these kinds of problems,” he says. “To me, it’s all about leveraging the powers of mathematics, discrete geometry and networks to produce optimal outcomes.”
Discrete geometry is a core area of mathematics that investigates the properties of geometric shapes in two, three and higher dimensions. Using discrete geometry, a huge variety of real-life optimization problems can be reduced to study geometric shapes called polytopes (high dimensional triangles, squares, polygons), allowing mathematicians to uncover what is considered a problem’s optimal solution.
High dimensional geometry can unlock complex mysteries
As part of his research, Khan aims to better understand the properties of such polytopes. Unlocking these mysteries would result in improving the speed at which optimal solutions are found for large-scale problems.
“In today’s complex and dynamic world, it is not unusual to encounter optimization problems involving thousands of variables,” explains Khan. “Solving these problems by hand is impossible and can even be challenging for the most powerful of computers.
“My goal is to develop robust discrete geometry theories that could support the development of powerful new algorithms to increase the processing capabilities of computers and help with the rapid identification of optimal solutions.”
For Khan, the appeal of discrete geometry lies in its difficulty and applicability.
“On the one hand, I am being challenged by problems that have been puzzling mathematicians for decades, while on the other, I can immediately see the practical benefits of my research contributions,” adds Khan, who will conclude his degree in 2017.
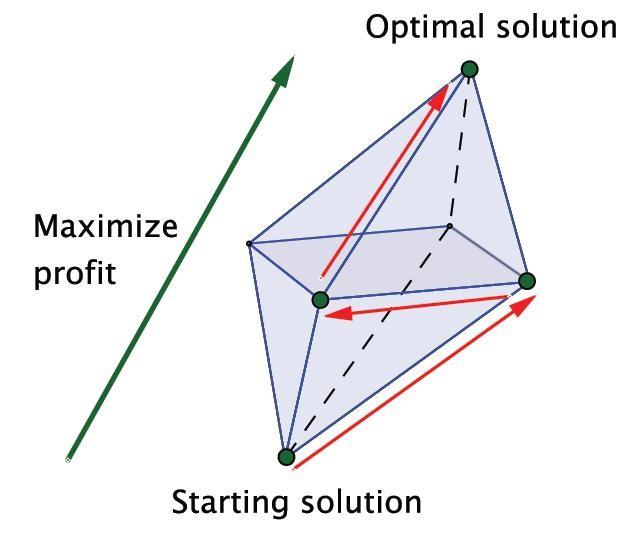
The best solution corresponds to a corner of a polytope, in this case a titled octahedron.
Muhammad Ali Khan
Resident expert drew Khan to Calgary
Khan’s research work is being supervised by Prof. Károly Bezdek, Tier I Canada Research Chair and Director of Centre for Computational and Discrete Geometry. Bezdek is a leader in the area of discrete and computational geometry — with one of his greatest achievements being proving the Planar Kneser-Poulsen Conjecture that had been unresolved for half a century. It was the desire of working with Prof. Bezdek that brought Khan to Calgary in the first place.
“If you run a Google search for ‘Discrete Geometry’ or ‘Computational Geometry’ our centre is the very first research group to show up,” says Khan excitedly. “Indeed, without Prof. Bezdek’s guidance and the centre’s support, I wouldn’t be where I am today.”
Khan’s fascination for geometry and optimization has produced tangible dividends — not only in terms of research output but also with respect to recognition.
In his short career, Khan has already published more than 25 journal and conference papers and has worked on multiple book chapters. This year alone, he has earned a Killam Scholarship, the Eric Milner Prize, the Dean’s Entrance Scholarship, the Departmental Recruitment Scholarship and the Departmental Teaching Excellence Award for TAs (both in fall and winter).
Mentor, ambassador, dedicated community member
In addition to thriving in his research and teaching work, Khan is a dedicated community member, managing and promoting the scientific activities of the Centre for Computational and Discrete Geometry at the University of Calgary.
He also participates in various mentoring activities organized by the Graduate Leaders Circle and he is the technical editor for Contributions to Discrete Mathematics — the journal published by the Department of Mathematics and Statistics in the Faculty of Science.
“What motivates me in all I do is my ambition to be a leading mathematician and an ambassador for my profession,” says Khan. “Mathematics is highly relevant to our lives and I intend to make it even more so. This recent Vanier Award certainly encourages me to continue to push myself more than ever.”
